Algoritm

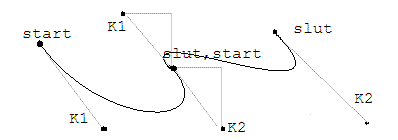
En Bezier-kurva definieras av 4 punkter: start, K1,K2, slut
Kurvan börjar i start, skjuter iväg mot K1 och slutar i slut, längs en linje från K2 till slut.

Genom att sätta ihop flera kurvor, fås fler böjar och en roligare kurva.
När man lägger till en ny kurva blir dess start densamma som den tidigare kurvans slut och den nya K1 bör väljas som den gamla K2 speglad i start. (På detta sätt blir kurvan kontinuerlig, d.v.s. utan "hack".)

Matematiken bakom Bezier-kurvan
En punkt P på kurvan mellan startoch slut ges av funktionen:

    P(t) = a*start + b*K1 + c*K2 +d*slut
        

    a= (1-t)*(1-t)*(1-t)
    b= 3*(1-t)*(1-t)*t
    c= 3*(1-t)*t*t
    d= t*t*t
        

    P(0) == start
    P(1) == slut
    P(0.25) == P(1/4) ==
        a= (1-1/4)*(1-1/4)*(1-1/4) == 27/64   (0.42)
        b= 3*(1-1/4)*(1-1/4)*1/4   == 27/64   (0.42)
        c= 3*(1-1/4)*1/4*1/4       ==  9/64   (0.14)
        d= 1/4*1/4*1/4             ==  1/64   (0.02)
        -->
        P(1/4) = 27/64*start + 27/64*K1 + 9/64*K2 + 1/64*slut
        

Om vi vill ha koordinaterna för punkten P(0.25)= (x,y), skriver vi:

        x= 0.42*start.x + 0.42*K1.x + 0.14*K2.x + 0.02*slut.x
        y= 0.42*start.y + 0.42*K1.y + 0.14*K2.y + 0.02*slut.y